I started using haskell-src-exts recently to parse Haskell files to turn them into LaTeX for The Joy of Haskell. I wasn’t used to this sort of parser that produces an AST that’s mapped back to the source file by line and column numbers, so it took me a while to wrap my head around what to do with its output.
After a while, I settled on some types, invented some terminology, and published a library: loc. Here’s an example to serve as an overview of the concepts:
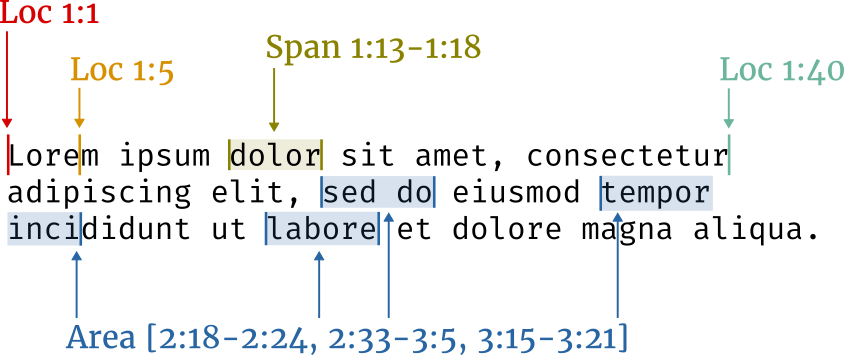
Loc— a cursor position, starting at the origin1:1Span— a nonempty contiguous region between two locsArea— a set of zero or more spans with gaps between them
Pos
Since all of the numbers we’re dealing with in this domain are positive, I
introduced a “positive integer” type. This is a newtype for Natural that
doesn’t allow zero.
newtype Pos = Pos Natural
deriving (Eq, Ord)
instance Num Pos where
fromInteger = Pos . checkForUnderflow . fromInteger
Pos x + Pos y = Pos (x + y)
Pos x - Pos y = Pos (checkForUnderflow (x - y))
Pos x * Pos y = Pos (x * y)
abs = id
signum _ = Pos 1
negate _ = throw Underflow
checkForUnderflow :: Natural -> Natural
checkForUnderflow n =
if n == 0 then throw Underflow else nI’d love to have toInteger :: Pos -> Integer from the Integral typeclass;
unfortunately, Integral is seriously overburdened class, and that would
require also implementing quotRem. I don’t terribly mind that negate throws
Underflow, but quotRem :: Pos -> Pos -> (Pos, Pos) is a level of nonsense
that crosses a line for me.
Instead I introduced my own ToNat class that I can use to convert positive
numbers to natural numbers. (My opinion that great typeclasses only have one
method continues to solidify.)
class ToNat a where
toNat :: a -> Natural
instance ToNat Pos where
toNat (Pos n) = nLine, Column
We then add some newtypes to be more specific about whether we’re talking about line or column numbers.
newtype Line = Line Pos
deriving (Eq, Ord, Num, Real, Enum, ToNat)
newtype Column = Column Pos
deriving (Eq, Ord, Num, Real, Enum, ToNat)Loc
A Loc is a Line and a Column.
data Loc = Loc
{ line :: Line
, column :: Column
}
deriving (Eq, Ord)Span
A Span is a start Loc and an end Loc.
data Span = Span
{ start :: Loc
, end :: Loc
} deriving (Eq, Ord)A Span is not allowed to be empty; in other words, start and end must be
different. I don’t have an extremely compelling rationale for this, other than
that empty spans didn’t make sense for my use case. Eliminating empty spans
also, in my opinion, seems to eliminate some ambiguity when we describe an
Area as a set of Spans.
There are two functions for constructing a Span. They both reorder their
arguments as appropriate to make sure the start comes before the end (so that
spans are never backwards). They take different approaches to ensuring that
spans are never empty: the first can throw an exception, whereas the second is
typed as Maybe.
fromTo :: Loc -> Loc -> Span
fromTo a b =
maybe (throw EmptySpan) id (fromToMay a b)
fromToMay :: Loc -> Loc -> Maybe Span
fromToMay a b =
case compare a b of
LT -> Just (Span a b)
GT -> Just (Span b a)
EQ -> NothingAs you can see here, I am not strictly opposed to writing partial functions in Haskell. I have two conditions for this, though:
- If a function can throw an exception, that fact must be clearly documented.
- A function that can throw an exception should be paired with a corresponding total function that does the same thing without the possibility of an exception.
In other words, providing a partial function that might be more convenient in some cases is fine, but don’t force a user of your API to use a partial function.
Area
An Area is conceptually a set of Spans, so in my first attempt that’s
exactly how I defined it.
newtype Area = Area (Set Span)Unfortunately I couldn’t manage to write reasonably efficient union and difference operations with this representation. Here’s what I ended up with instead:
data Terminus = Start | End
deriving (Eq, Ord)
newtype Area = Area (Map Loc Terminus)
deriving (Eq, Ord)Rather than keeping a set of the spans, we keep a set of the spans’ start and
end positions, along with a tag indicating whether each is a start or an end.
You should notice the drawback to this representation: it is now much less
“correct by construction”. The map must contain an even number of Locs,
alternating between Start and End. Any operations we write using the Area
constructor must take care to preserve that property.
I’ll only cover one of the algorithms in this blog post: Adding a Span to an
Area. We’re going to define a function with this type:
addSpan :: Span -> Area -> AreaData.Map in the containers package provides an O(log n) operation to
divide a map into keys that are less than and greater than some key:
split :: Ord k => k -> Map k a -> (Map k a, Map k a)We’re going to use the split function twice: to split the area into Locs
that come before the start of the span we’re adding, and Locs that come
after the end of the span we’re adding. Then we’ll combine the stuff in the
middle with the new span, and finally mappend all the maps back together.
addSpan :: Span -> Area -> Area
addSpan b (Area as) =
let
-- Spans lower than b that do not abut or
-- overlap b. These spans will remain
-- completely intact in the result.
unmodifiedSpansBelow :: Map Loc Terminus
-- Spans greater than b that do not abut
-- or overlap b. These spans will remain
-- completely intact in the result.
unmodifiedSpansAbove :: Map Loc Terminus
-- The start location of a span that starts
-- below b but doesn't end below b, if such
-- a span exists. This span will be merged
-- into the 'middle'.
startBelow :: Maybe Loc
-- The end location of a span that ends
-- above b but doesn't start above b, if
-- such a span exists. This span will be
-- merged into the 'middle'.
endAbove :: Maybe Loc
-- b, plus any spans it abuts or overlaps.
middle :: Map Loc Terminus
(unmodifiedSpansBelow, startBelow) =
let
(below, _) = Map.split (Span.start b) as
in
case Map.maxViewWithKey below of
Just ((l, Start), xs) -> (xs, Just l)
_ -> (below, Nothing)
(unmodifiedSpansAbove, endAbove) =
let
(_, above) = Map.split (Span.end b) as
in
case Map.minViewWithKey above of
Just ((l, End), xs) -> (xs, Just l)
_ -> (above, Nothing)
middle = Map.fromList
[ (minimum $ Foldable.toList startBelow
<> [Span.start b], Start)
, (maximum $ Foldable.toList endAbove
<> [Span.end b], End)
]
in
Area $ unmodifiedSpansBelow
<> middle
<> unmodifiedSpansAboveShow
I defined custom Show and Read instances to be able to write terse
doctests like
>>> addSpan (read "1:1-6:1") (read "[1:1-3:1,6:1-6:2,7:4-7:5]")
[1:1-6:2,7:4-7:5]I usually just implement show when I write a custom Show instance, but this
time I thought I’d do it the right way and implement showsPrec instead. This
difference list construction avoids expensive O(n) list concatenations.
locShowsPrec :: Int -> Loc -> ShowS
locShowsPrec _ (Loc l c) =
shows l .
showString ":" .
shows c
spanShowsPrec :: Int -> Span -> ShowS
spanShowsPrec _ (Span a b) =
locShowsPrec 10 a .
showString "-" .
locShowsPrec 10 bRead
This was the first time I really explored Read in-depth. It’s a little rough,
but surprisingly usable (despite not great documentation).
The parser for Pos is based on the parser for Natural, applying mfilter (/=
0) to make the parser fail if the input represents a zero.
posReadPrec :: ReadPrec Pos
posReadPrec =
Pos <$> mfilter (/= 0) readPrecAs a reminder, the type of mfilter is:
mfilter :: MonadPlus m => (a -> Bool) -> m a -> m aThe Loc parser uses a very typical Applicative pattern:
-- | Parses a single specific character.
readPrecChar :: Char -> ReadPrec ()
readPrecChar = void . readP_to_Prec . const . ReadP.char
locReadPrec :: ReadPrec Loc
locReadPrec =
Loc <$>
readPrec <*
readPrecChar ':' <*>
readPrecWe used mfilter above to introduce failure into the Pos parser; for Span
we’re going to use empty.
empty :: Alternative f => f aFirst we use fromToMay to produce a Maybe Span, and then in the case where
the result is Nothing we use empty to make the parser fail.
spanReadPrec :: ReadPrec Span
spanReadPrec =
locReadPrec >>= \a ->
readPrecChar '-' *>
locReadPrec >>= \b ->
maybe empty pure (fromToMay a b)That’s all folks
This wasn’t intensely exciting or weird, but I want to produce more blog posts about doing normal stuff in Haskell. The package is called [loc] on Hackage if you’d like to investigate further.
The build tools for The Joy of Haskell are turning into an interesting custom reinvention of Literate Haskell; stay tuned for updates on that!
Addendum
would it maybe make it easier to interpret Loc as a character position (à la vim)? then Span with start=end can be a 1-char span and there are no invalid ones
This is a nice suggestion, and “no invalid spans” is an appealing pitch. The idea is that we could represent a span using two inclusive bounds [start, end] rather than an inclusive and an exclusive bound [start, end). Unfortunately, it would end up complicating the API a bit.
Currently, the library is entirely agnostic of the text that the positions are
referring to. This means there is no “plus one” operation on Loc, because the
next Loc after 4:17 could be either 4:18 or 5:1 — we can’t tell without
knowing the line lengths. Therefore, with inclusive ranges, you can’t tell
whether span 4:16-4:17 abuts span 5:1-5:2 — at least, not without knowing
whether the character at position 4:17 is a newline.