This project for CS 6491 (computer graphics) uses Scala with JOGL to generate a tree over approximately half of the faces of a triangle manifold using a laced ring construction, and then render an animation resembling a vine that grows upward along paths defined by the tree.
Links: Source, animation, paper, slides.
Mesh structure
The mesh is stored as a collection of components, where each component
is a collection of triangles, and each triangle consists of three corners.
The data comes from the Stanford Bunny read from a ply file.
Basic rendering with mesh edges drawn:

Each new triangle t added to the mesh initially belongs to its own new component. If it is adjacent to another triangle u, then the components of t and u are merged into a single component. When two components merge, one of them may have its triangles reversed to ensure consistent corner ordering among all of the triangles within each component.
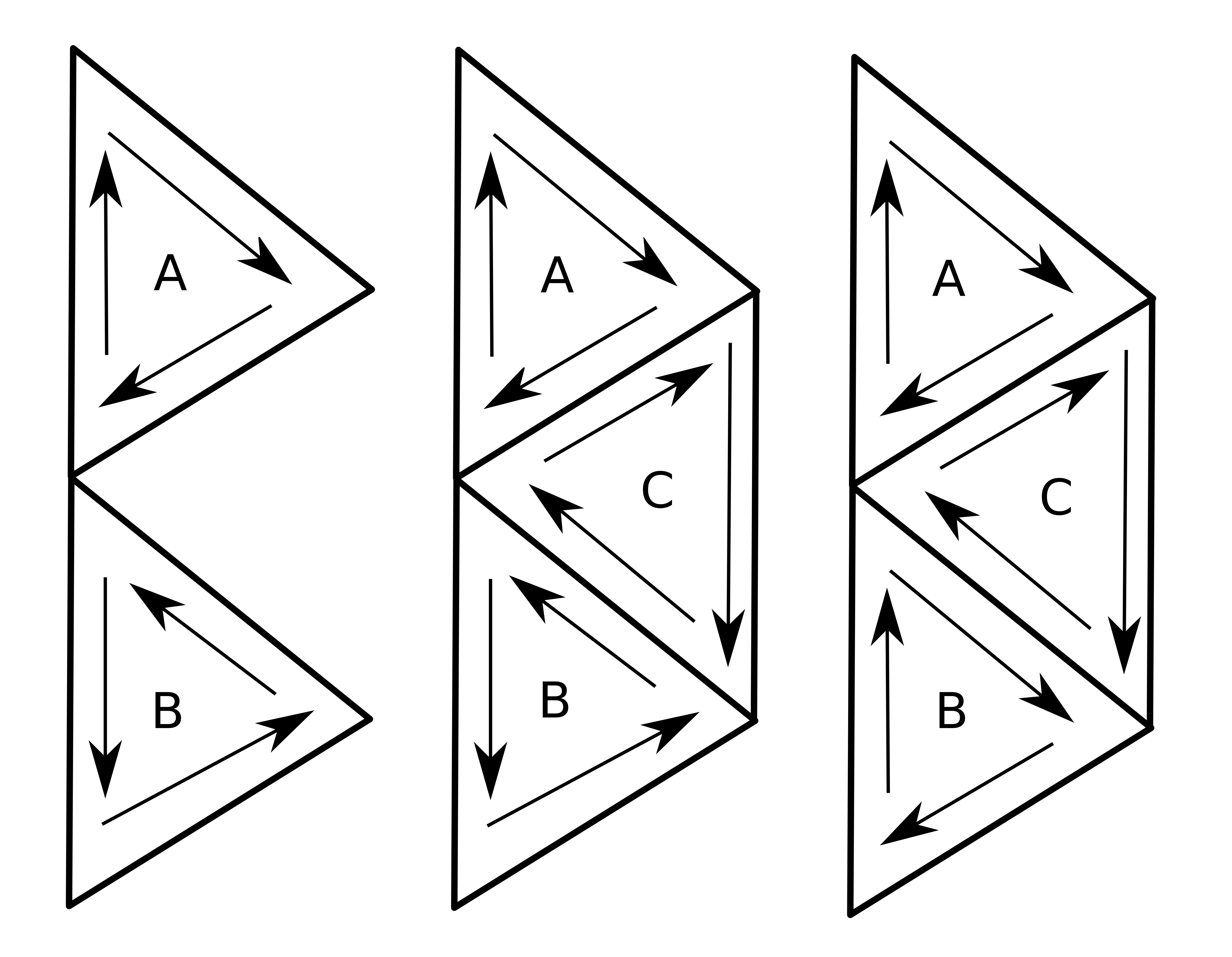
When triangle C is added to this mesh, its component is merged with A and then with B. A and B already have compatible ordering. B and C, however, do not, indicated by the observation that their shared edges point in the same direction. This is resolved by reversing the order of the corners in C.
Triangle forest
The first task is to construct an undirected acyclic graph of triangles (rendered as the darker color below). The graph is initialized with a triangle located near the bottom-center of the model space, and is subsequently expanded by conducting a traversal of the mesh, rejecting triangles that share any edges with a triangle already in the graph. A breadth-first strategy was chosen over depth-first to exhibit more vine-like behavior.
Demonstration of LR result:

The darker-colored surface indicates triangles that belong to the tree. The resulting psuedo-Hamiltonian cycle is drawn in black.
Segments of the vine are defined over triplets of consecutive triangles. For example, the sequence of triangles (ABC, BCD, CDE) corresponds to a vine segment from the midpoint of BC to the midpoint of CD.
The bunny is slightly sunken into the mud puddle so that its bottommost vertices are “underground”. The triangle tree is split into a triangle directed forest, where the underground nodes are used as the tree roots. This ensures that all the vine segments sprouting from the ground do so simultaneously at the beginning of the animation.
Vine rendering
The vine itself is rendered by using gluCylinder to construct each segment.
The thickness of each segment is manipulated to create a vine that is thicker
at its roots and grows over time. Thickness is calculated as
(c1 + c2 atan(α + c3) +
c4 atan(-β + c5)) t,
where the c are constants, α is the maximum distance from the node
to any leaf in the tree, β is the distance from the node
to the root of the tree, and t is the time.
Screenshots from the animation:

